-
难度：
使用次数：119
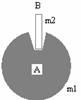
入库时间：2014-11-10下面是一个物理演示实验，它显示：图中自由下落的物体A和B经反弹后，B能上升倒比初始位置高得多的地方。A是某种材料做成的实心球，质量m1=0.28kg，在其顶部的凹坑中插着质量m2=0.10kg的木棍B。B只是轻轻地插在凹坑中，其下端与坑底之间有小空隙。将此装置从A下端离地板的高度H=1.25m处由静止释放。实验中，A触地后在极短时间内反弹，且其速度大小不变；接着木棍B脱离A开始上升，而球A恰好停留在地板上，求B上升的高度。（g=10m/s2）
-
难度：
使用次数：140
入库时间：2014-11-10
俄罗斯“和平号”空间站在人类航天史上写下了辉煌的篇章，因不能保障其继续运行，3月20号左右将坠入太平洋.设空间站的总质量为ｍ，在离地面高度为ｈ的轨道上绕地球做匀速圆周运动坠落时地面指挥系统使空间站在极短时间内向前喷出部分高速气体，使其速度瞬间变小，在万有引力作用下下坠.设喷出气体的质量为
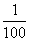m，喷出速度为空间站原来速度的37倍，坠入过程中外力对空间站做功为W.求：(1)空间站做圆周运动时的线速度.
(2)空间站落到太平洋表面时的速度.
(设地球表面的重力加速度为ｇ，地球半径为R)
-
难度：
使用次数：101
入库时间：2014-11-10
如图甲，A、B两板间距为
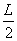，板间电势差为U，C、D两板间距离和板长均为L，两板间加一如图乙所示的电压.在S处有一电量为q、质量为m的带电粒子，经A、B间电场加速又经C、D间电场偏转后进入一个垂直纸面向里的匀强磁场区域，磁感强度为B.不计重力影响，欲使该带电粒子经过某路径后能返回S处.求：(1)匀强磁场的宽度L′至少为多少?
(2)该带电粒子周期性运动的周期T.
-
难度：
使用次数：144
入库时间：2014-11-10
1951年，物理学家发现了“电子偶数”，所谓“电子偶数”就是由一个负电子和一个正电子绕它们的质量中心旋转形成的相对稳定的系统.已知正、负电子的质量均为me，普朗克常数为h，静电力常量为k，假设“电子偶数”中正、负电子绕它们质量中心做匀速圆周运动的轨道半径r、运动速度v及电子的质量满足量子化理论：2mevnrn=nh/2π，n=1,2……，“电子偶数”的能量为正负电子运动的动能和系统的电势能之和，已知两正负电子相距为L时的电势能为Ep=-k
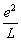，试求n=1时“电子偶数”的能量. -
难度：
使用次数：142
入库时间：2014-11-10
如图12是用高电阻放电法测电容的实验电路图，其原理是测出电容器在充电电压为U时所带的电荷量Q，从而求出其电容C.该实验的操作步骤如下：①按电路图接好实验电路;②接通开关S，调节电阻箱R的阻值，使微安表的指针接近满刻度，记下这时的电压表读数U0＝6.2 V和微安表读数I0＝490 μA;③断开电键S并同时开始计时，每隔5 s或10 s读一次微安表的读数i,将读数记录在预先设计的表格中;④根据表格中的12组数据，以t为横坐标，i为纵坐标，在坐标纸上描点(图中用“×”表示),则：
(1)根据图示中的描点作出图线.
(2)试分析图示中i-t图线下所围的“面积”所表示的物理意义.
(3)根据以上实验结果和图线，估算当电容器两端电压为U0所带的电量Q0，并计算电容器的电容.
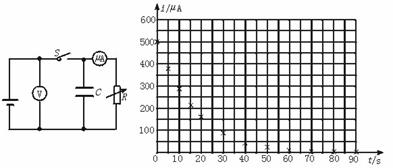
图12