-
难度：
使用次数：132
入库时间：2020-12-15小萱在探究某个力学问题时，通过实验得到如下表所示的实验数据，请根据表中数据归纳出拉力F与体积V的关系：F＝________．
-
难度：
使用次数：133
入库时间：2020-12-15
小阳在探究某种物质量与体积的关系时，得到如下表所示的实验数据．请根据表中数据归纳出m与V的关系：m=__________．
-
难度：
使用次数：175
入库时间：2020-12-15
提出问题:小明看到一则新闻:我国具有自主知识产权的“海燕”无人水下滑翔机刷新了下潜深度的最新世界纪录，思考:水下滑翔机是怎样实现浮沉的?
猜想与假设:可能和鱼一样，鱼鳔中气体总质量不变，通过鱼体自身的压缩来改变体积实现沉浮的．
设计实验:他设计了如图甲所示的实验．他想通过观察液面的位置变化来证实自己的想法．结果，小明的设计遭到了小李的否定，小李要求小明将设计改为如图乙所示的结构：在鱼缸中灌满水，并加带有细管的盖密封，通过观察细管中液面的变化来观察鱼体积的变化．
评估与交流:
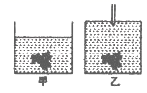
(1)当鱼体积缩小时，图甲中的水面变化是________（选填“不变”、“上升”或“下降”）原来悬浮的鱼将__________（选填“上浮”或“下沉”）．
(2)小李要求小明用图乙进行实验的主要好处是:更易于观察的鱼_______变化．我们学过的_______（填仪器名称）设计也用到了这种方法．
(3)假如一个从水底鱼口中吐出的空气泡泡，在上升至水面的过程中(破裂之前)，其浮力大小应该（_______）
A．不变
B．越来越大
C．越来越小
D．先不变后变小
(4)水下滑翔机是怎样实现浮沉的呢?小李上网査找，得知水下滑翔机浮力引擎的外部装有一个气囊，引擎将油压进或压出该气囊，随着气囊的变大或变小，实现浮沉．从物体的浮沉条件分析，水下滑翔机是靠改变__________实现浮沉的，与潜水艇实现浮沉的方法__________（选填“相同”或“不同”）．
-
难度：
使用次数：117
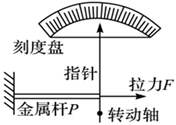
入库时间：2020-12-15
科学研究表明：金属杆受到拉力会伸长，在一定范围内，金属杆的伸长与它所受到的拉力F成正比．现有一金属杆，长为8m，横截面积为0.4cm2，实际使用时要求金属杆受到拉力后的伸长不超过0.4cm．由于直接对这一金属杆测试有困难，故选用同种材料制成的样品进行测试，测试时样品所受的拉力始终为2000N，通过测试取得数据如下．
长度l（m）
横截面积cm2
伸长cm
1
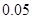
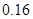
2
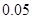
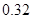
1
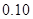
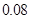
4
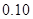
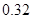
4
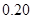
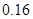
请分析表中数据回答下列问题：
（1）在对样品进行测试时，采用如图所示的装置，这样设计有何优点？答：______．
（2）分析样品测试数据可知，金属杆伸长的长度（伸长量）跟它的长度和______有关．
（3）根据（2）及金属杆的伸长量还与它所受到的拉力F成正比，可以得到金属杆伸长量的表达式ΔL =______．
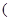比例系数用k表示，拉力，长度和横截面积分别用F、L和S表示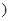
（4）该金属杆P能够承受的最大拉力为______N．
-
难度：
使用次数：175
入库时间：2020-12-15
请阅读《物理实验中的图象法》回答问题．
物理实验中的图象法
物理实验中的图象法是一种整理、分析数据的有效方法，图象中的图线可直观、简洁地显示出因变量随着自变量变换的趋势或规律．如果想要将物理实数据绘制成图象，可以按照下面的步骤来进行．
第一步，建立坐标轴、标注物理量和设定分度．首先建立坐标轴，通常用横轴代表自变量，纵轴代表因变量，在坐标轴上分别标注自变量和因变量的名称及单位；然后，设定坐标分度值．为了使绘制的图线比较均匀地分布在整幅坐标纸上，而不要偏在一角或一边，坐标分度值可以不从零开始．在一组数据中，自变量与因变量均有最低值和最高值，分度时，可用低于最低值的某一整数值作起点，高于最高值的某一整数值作终点．
第二步，根据数据描点．描点时根据数据在坐标纸上力求精准地画出对应的点．
第三步，绘制图线．绘制图线时不要把数据点逐点连接成折线，而应依据数据点的整体分布趋势，描绘出一条直线或光滑曲线，让尽可能多的点在图线上，或让数据点比较均匀地分布在图线两旁，这样绘制出的图线比图上的任何一个数据点更适合作为进行分析预测的依据．
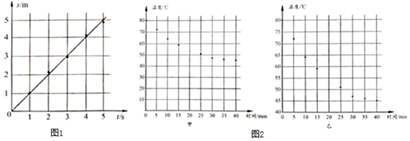
倒如，小宇记录了自己沿直线步行过程中的时间及所对应的路程，如图中的黑点是他根据记录的数据在坐标纸上描出的数据点，利用这些数据点绘制出了如图中的直线．利用这条直线可以清楚地看出小宇步行的过程近似为匀速运动，还可以利用图线上的点计算出小宇步行过程中的速度，进而用速度预测出他在某一段时间内步行的路程．
请根据上述材料，回答下列问题：
（1）根据如图所示的图象，预测小宇步行10s的路程为_____m．
（2）下表是某同学记录的物体温度随时间变化的实验数据．
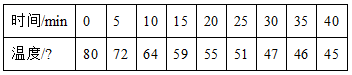
①若要绘制上述物体的温度随时间变化的图象，应选择如图中____图更合理．（选填“甲”或“乙”）
②请在你选择的图中描出第20min时的温度数据点，并绘制出本次实验中物体温度随时间变化的图线_____．
