-
难度：
使用次数：136
入库时间：2020-03-18演绎式探究﹣探究太阳的引力系数：
（1）宇宙中任何两个物体之间都存在万有引力，万有引力的大小F引=G
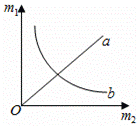
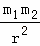，其中m1、m2分别为两个物体间的距离，万有引力常数G=6.67×10﹣11N•m2/kg2．物体间引力和距离一定时，两个物体质量m1、m2分的关系可以用如图中图线 来表示．（2）行星绕恒星的运动可以近似地看作匀速圆周运动．行星受到一个恒定的指向恒星的向心力，向心力的大小F向=mω2r，其中m为行星质量，r为两星之间的距离，ω为行星做圆周运动的角速度，其大小等于单位时间内行星与恒星连线转过的角度．行星绕恒星运动一周所用的时间用周期T表示，角速度ω与转动周期T的关系为：ω=
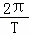．行星所受向心力F向的大小等于恒星对行星的引力F引的大小．每个星球对在它表面附件的物体都存在引力，引力与物体质量的比值叫作引力系数，用g表示，我们学过地球的引力系数g地=10N/kg．对于每个星球来讲，下列公式成立：R2g=GM，其中R为星球半径，g为星球引力系数，M为星球质量，万有引力常数G=6.67×10﹣11N•m2/kg2．
已知地球质量为m，地球到太阳的距离为L，太阳半径为R，地球的公转周期为T．请你推导出太阳的引力系数g日=
．
-
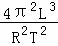难度：
使用次数：77
入库时间：2020-03-18
液体内部存在压强。如图所示，烧杯内盛有密度为
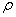的液体，我们可以设想液面下h深处有一面积为s的水平圆面，它所受到的压力是其上方圆柱形的小液柱所产生的。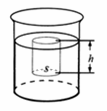
（1）请在图中作出小液柱所受重力的示意图。
（2）请推证：液体内部深度为h处的压强
。 -
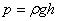难度：
使用次数：131
入库时间：2020-03-18
斜面是人们生产和生活中经常使用的一种可以省力的简单机械。下面是某同学针对斜面问题进行的理论研究的过程。请你帮他完成“理论论证”。
提出问题：使用斜面为什么可以省力？
建立模型：如图所示，斜面的长为L，高为h，沿光滑斜面匀速向上拉动重为G的物体，所用拉力为F。
理论论证：运用功的原理证明:F<G。
-
难度：
使用次数：98
入库时间：2020-03-18
在底面积为S的薄壁柱形容器内注入适量的水，让空烧杯漂浮在水面上，测出水的深度为h0，如图所示：再将一金属球放入烧杯中，此时烧杯仍漂浮在水面上，测出水的深为h1，最后将该金属球取出放入水中（空烧杯仍漂浮在水面上，待金属球沉底后测出水的深度为h2，已知水的密度为ρ水，请你推导：
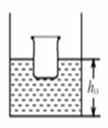
（1）金属球的密度为ρ球= ρ水（h1-h0）/（h2-h0）
（2）金属球沉底后，它对容器底的压力为F=ρ水g（h1-h2）S
-
难度：
使用次数：141
入库时间：2020-03-18
求证在串联电路中，串联电路的总电阻，等于各导体的电阻之和．