-
难度：
使用次数：117
入库时间：2014-11-05如图24-19所示，两端开口的圆筒内嵌有一凸透镜，透镜主光轴恰好与圆筒中轴线重合。为了测出该透镜的焦距以及透镜在圆筒内的位置，小李同学做如下实验：在圆筒左侧凸透镜的主光轴上放置一点光源S，在圆筒右侧垂直凸透镜的主光轴固定一光屏，点光源S与光屏的距离为L。左右移动圆筒，当圆筒左端面距离点光源S为a时，恰好在光屏上成一个清晰的像；将圆筒向右水平移动距离b，光屏上又出现了一个清晰的像。则凸透镜和圆筒左端面的距离x为_____，该透镜的焦距f为__________。
-
难度：
使用次数：113
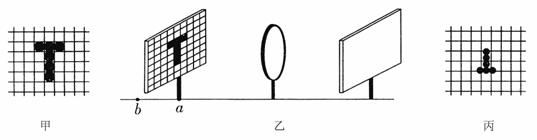
入库时间：2014-11-05
小明在“探究凸透镜成像规律”实验中，用装有6个发光二极管的有方格的白纸板做发光物体，如图甲所示.又用这种有同样大小方格的白纸板做光屏.将发光物体、凸透镜和光屏组装到光具座上并调整好.
（1）当发光物体在
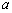点时，如图乙所示，在光屏上成的像如图丙所示.则光屏上的像是倒立、________的实像.将发光物体由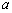点移动到
点，要想找到像的位置，应移动光屏，直到____________为止.（2）用这种发光物体和光屏做实验，最主要的一条优点是：___________________.
（3）如图乙所示，当发光物体在
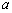点时，物与像之间的距离为S1，当发光物体在点时，物与像之间的距离为S2，则S1 S2.(选填“>”、“=”或“<”)（4）小明探究完凸透镜成像规律后，接着又做了一个观察实验.发光体位置不变，取下光屏，当眼睛在原光屏处会看到发光体的像吗？＿＿＿＿＿＿＿＿＿＿＿＿，眼睛靠近凸透镜，是否能看到像？＿＿＿＿.眼睛从原光屏位置远离凸透镜，是否能看到像？＿＿＿＿＿＿。（填“能看到”或是“不能看到”）
-
难度：
使用次数：139
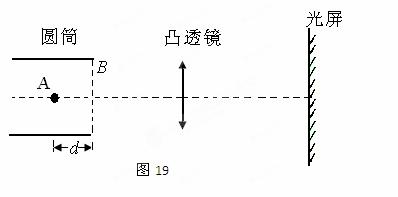
入库时间：2014-11-05
如图 19所示，一点光源位于金属圆筒内部轴线上A点。圆筒轴线与凸透镜主光轴重合，光屏与圆筒轴线垂直且距离透镜足够远。此时，点光源正好在光屏上形成一个清晰的像，测出此时凸透镜与圆筒右端面B的距离为L；向右移动凸透镜到适当位置，光屏上再次出现了清晰的像。由于光源位于圆筒的内部，无法直接测量出A与筒右端面的距离d，为了求出d的大小，在上述过程中还需要测量出的一个物理是 ；如果用N来表示该物理量的大小，则可以得出d= 。
-
难度：
使用次数：101
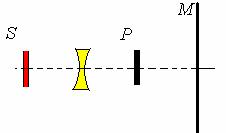
入库时间：2014-11-05
如图所示，不透光小圆盘P和小圆形发光面S的半径均为R，平行竖直放置，二者相距为2d。在它们正中间放置一个焦距为2d的凹透镜，透镜的主光轴通过P和S的圆心。在P的右侧相距d处，放置一平行于圆盘面的光屏M（足够大）。则不透光圆盘P在光屏M上形成的本影（发光面S发出的任何光线都不能进入该区域内）面积为______________；不透光圆盘P在光屏M上形成的半影（发光面S发出的光线中只有部分能进入该区域内）面积为______________。
-
难度：
使用次数：53
入库时间：2014-11-05
说出两种最简便的估测凸透镜焦距的方法。